Regresyon analizi nedir? Bir değişkenin (bağımlı değişken) başka bir veya daha fazla değişken (bağımsız değişken) ile olan ilişkisini modellemeye yönelik istatistiksel bir yöntemdir. Temel amacı, bağımlı değişkenin değeri ile bağımsız değişkenlerin değeri arasındaki ilişkiyi belirlemek ve bu ilişkiyi kullanarak tahminlerde bulunmaktır. Regresyon analizi, özellikle ekonomi, mühendislik, sosyal bilimler ve sağlık gibi birçok alanda yaygın olarak kullanılır. Bu yöntem, bir olayın veya durumun belirli faktörlerle nasıl etkileşime girdiğini anlamak için güçlü bir araçtır.

Regresyon Analizi Nedir?

1. Regresyon Analizinin Temel Bileşenleri

Regresyon analizinde üç temel öğe vardır:

Bağımlı Değişken (Y): Tahmin edilmek istenen değişken. Örneğin, bir şirketin yıllık karı veya bir öğrencinin sınav puanı.
Bağımsız Değişkenler (X): Bağımlı değişkeni etkileyen değişkenler. Bu değişkenler, bir modelde sonuçları etkileyebilecek faktörleri temsil eder. Örneğin, öğrencinin sınav puanını etkileyen faktörler; çalışma saati, yaş, ders içeriği olabilir.
Model: Bağımlı değişken ile bağımsız değişkenler arasındaki ilişkiyi matematiksel bir şekilde ifade eden formül. Regresyon analizinin amacı bu modelin en uygun parametrelerini bulmaktır.

Regresyon Analizi Nedir?

2. Regresyon Analizinin Çeşitleri

a. Doğrusal Regresyon (Linear Regression)

Doğrusal regresyon en temel regresyon türüdür. Bu model, bağımlı değişkenin bağımsız değişkenlerle doğrusal bir ilişki içinde olduğunu varsayar. Yani, değişkenler arasındaki ilişki bir doğruyla ifade edilebilir. Regresyon Analizi Nedir? Aslında bazı formüllerle ifade edilse de hesaplamadan çok yorumlamaya dayanır.

Doğrusal regresyon modeli şu şekilde ifade edilir:

$Y=β0+β1X+ϵ$

Burada:

$YY$ bağımlı değişkeni,
$XX$ bağımsız değişkeni,
$β0\beta_0$ sabit terimi (intercept),
$β1\beta_1$ regresyon katsayısını (slope) ifade eder,
$ϵ\epsilon$ ise hata terimidir.

Örnek: Bir şirketin gelirinin, reklam harcaması ile olan ilişkisini anlamak için doğrusal regresyon kullanılabilir. Burada reklam harcaması bağımsız değişken (X), gelir ise bağımlı değişken (Y) olacaktır.

b. Çoklu Doğrusal Regresyon (Multiple Linear Regression)

Çoklu doğrusal regresyon, birden fazla bağımsız değişkenin etkisini incelemek için kullanılır. Bu model, bağımlı değişkenin birden fazla faktör tarafından etkilendiği durumlarda kullanılır. Regresyon Analizi Nedir? Karmaşık bir formül gibi görünse de excell gibi uygulamalarla bile kolayca hesaplanabilir.

Model şu şekilde ifade edilir:

$Y=β0+β1X1+β2X2+\dots+βnXn+ϵ$

Burada, $X1,X2,…,XnX_1, X_2, \dots, X_n$ bağımsız değişkenlerdir. Örneğin, bir evin fiyatını tahmin etmek için evin büyüklüğü, yaşı, konumu gibi birden fazla bağımsız değişkeni dikkate alan bir model oluşturulabilir.

c. Lojistik Regresyon (Logistic Regression)

Lojistik regresyon, bağımlı değişkenin kategorik olduğu durumlarda kullanılır. Bu model, özellikle sınıflandırma problemleri için uygundur ve bağımlı değişkenin iki veya daha fazla kategoriye ayrıldığı durumlar için kullanılır.

Model şu şekilde ifade edilir:

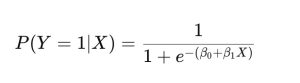
$P(Y=1/X)=1/1+e-(β0+β1X)$

Burada $P(Y=1/X)P(Y=1|X)$ , bağımlı değişkenin belirli bir sınıfa ait olma olasılığını ifade eder.

Örnek: Bir öğrencinin sınavdan geçip geçmeyeceğini tahmin etmek için lojistik regresyon kullanılabilir.

d. Polinomal Regresyon (Polynomial Regression)

Polinomal regresyon, bağımlı değişken ile bağımsız değişken arasındaki ilişki doğrusal olmadığında, ilişkiyi daha karmaşık bir polinom fonksiyonu ile modellemeye olanak tanır. Bu tür bir regresyon, veriler doğrusal olmayan bir yapıya sahipse kullanılır. Regresyon Analizi Nedir?

3. Regresyon Analizinde Kullanılan Önemli Kavramlar

a. R-Kare (R²)

R², modelin açıklayıcı gücünü ifade eden bir istatistiksel ölçüdür. Bu değer, bağımsız değişkenlerin bağımlı değişkenin varyansını ne kadar açıkladığını gösterir. R² değeri 0 ile 1 arasında değişir ve 1’e yaklaştıkça modelin daha iyi bir açıklama sunduğunu gösterir.

b. Hata Terimi (Error Term)

Regresyon modelinde yer alan hata terimi, tahmin edilen değer ile gerçek değer arasındaki farktır. İdeal bir regresyon modelinde bu farkın minimal olması beklenir.

c. Katsayılar (Coefficients)

Regresyon analizinde katsayılar, her bağımsız değişkenin bağımlı değişken üzerindeki etkisini gösterir. Bir bağımsız değişkenin katsayısı, bu değişkenin bir birimlik değişiminin bağımlı değişkeni ne kadar değiştireceğini gösterir. Regresyon Analizi Nedir?

d. P-Değeri (P-Value)

P-değeri, bağımsız değişkenlerin modeldeki anlamlılık seviyesini test etmek için kullanılır. Genellikle, p-değeri 0.05’ten küçükse, o değişkenin modelde anlamlı olduğu kabul edilir.

4. Regresyon Analizi Nerelerde Kullanılır?

Regresyon analizi, çok geniş bir uygulama alanına sahiptir. Bazı yaygın kullanım alanları şunlardır:

Ekonomi: Bir ülkenin ekonomik büyümesini etkileyen faktörleri modellemek.
Finans: Hisse senedi fiyatlarının, faiz oranları veya şirket performansı ile ilişkisini analiz etmek.
Pazarlama: Reklam harcamalarının satışlara etkisini analiz etmek.
Sağlık: Bir tedavinin, hastaların iyileşme süreci üzerindeki etkisini modellemek.
Sosyal Bilimler: Eğitim düzeyinin, gelir düzeyini etkileyip etkilemediğini analiz etmek. Regresyon Analizi Nedir?

5. Regresyon Analizinin Avantajları ve Sınırlamaları

Avantajları:

Basit ve anlaşılır: Regresyon analizi, karmaşık ilişkileri basit bir modelle ifade edebilir.
Tahmin: Regresyon, gelecekteki veriler için tahminlerde bulunma imkanı sağlar.
İlişkileri anlamak: Bağımsız değişkenlerle bağımlı değişken arasındaki ilişkiyi analiz etmek için güçlü bir araçtır.

Sınırlamaları:

Doğrusal ilişki varsayımı: Regresyon analizi genellikle doğrusal ilişkileri varsayar. Gerçek dünyadaki ilişkiler her zaman doğrusal olmayabilir.
Hassasiyet: Özellikle çoklu doğrusal regresyon analizlerinde, bağımsız değişkenler arasındaki yüksek korelasyon modelin doğruluğunu olumsuz etkileyebilir.
Outlier (Aykırı Değerler): Aykırı değerler, modelin parametrelerini bozabilir ve yanıltıcı sonuçlar verebilir.

Sonuç

Regresyon analizi, çeşitli alanlarda ilişkileri modellemek ve tahminlerde bulunmak için güçlü bir istatistiksel araçtır. Basit doğrusal regresyondan karmaşık çoklu doğrusal regresyona, lojistik regresyondan polinomal regresyona kadar birçok farklı türü vardır. Uygulama alanları geniştir ve her sektörde kullanılabilir. Ancak doğru sonuçlar elde etmek için modelin doğru şekilde seçilmesi, uygun veri toplama ve analiz süreçlerinin izlenmesi önemlidir. Regresyon analizi enerji etüt raporlarında PLANETUS tarafından standart olarak enerji analizi için yapılmaktadır. Regresyon Analizi Nedir? sorusuna cevap vermek istedik. Detaylı Enerji Etüt raporunda bulunması zorunlu olmamasına rağmen enerji tüketimleri ve verimlilik sonrası bu analiz hazırladığımız tüm raporlarda standart olarak yer almaktadır.

Regresyon Analizi Nedir?